レンズの開口数と分解能
目次
1.レンズの分解能とは
対象物を拡大して観察する場合、倍率はもちろん大切ですが、
細部をきちんと識別できることも重要です。
この能力のことを分解能といい、
「接近している2点を識別できる最小の距離」で表されます。
分解能=2点識別できる距離
*微小物の有無等の観察であれば、もっと小さいものも確認可能です。
数式に表すと 分解能=kλ/NA となります。
kは係数で 0.61や0.5 の値が使われます。
λは光の波長です。 通常の可視光であれば 0.55μmを使います。
NAはレンズの開口数です。(レンズの性能の1つを示す値です。)
開口数が大きい程、分解能が高く(数値は小さく)なります。
(例)開口数(NA)が0.9のレンズであれば、
分解能=0.5x0.55/0.9=0.30μm となります。
2点間が0.30μmであれば、2点識別できることになります。
分解能と倍率は関係ないので、このレンズでいくら倍率を上げても
2点間の識別は 0.30μmとなります。
2.レンズの開口数
レンズの性能を決める重要な数値です。
開口数(NA)=nsinθ
nは対象物からレンズまでの媒体の屈折率で空気ならば n=1です。
θは対象物と光軸が交差する1点からレンズに入る光のうち
一番外側になる角度です。
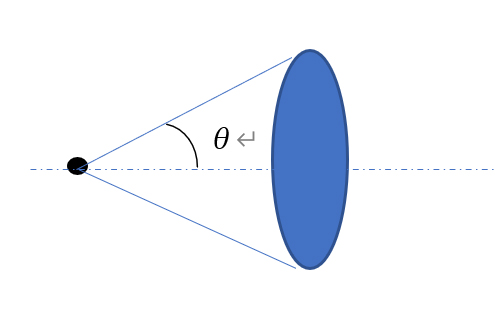
開口数が大きい程
明るいレンズとなります。
また、分解能=kλ/NA なので開口数が大きい程
分解能が高くなります。(数値は小さくなります。)
3.弊社メガピクセル対応テレセントリックレンズの事例

開口数が 0.026です。
分解能=(0.61x0.55)/0.026=12.9μmとなります。
上記の表の分解能(12.7μm)とほぼ一致します。
4.弊社中倍率ズームレンズの事例
弊社中倍率ズームレンズ(SDS-M)の開口数は
0.014(最低倍率時)から0.036(最大倍率時)となります。
最低倍率時分解能=(0.61x0.55)/0.014=23.9μm
最大倍率時分解能=(0.61x0.55)/0.036=9.3μm
となります。


